Selective review of offline change point detection methods-论文阅读
Date:
论文: 离线变化点检测方法的选择性综述
论文地址:https://arxiv.org/pdf/1801.00718.pdf
一.摘要
本文介绍了离线检测多元时间序列中多个变化点的算法的选择性调研。采用了一种普适而有结构的方法论策略来组织这个广泛的研究领域。具体而言,本综述中考虑的检测算法由三个要素来描述:代价函数、搜索方法和变化点数量的约束。对这些要素进行了描述、评估和讨论。本文还提供了在名为ruptures的Python软件包中实现的主要算法的实例。
二. 介绍
信号处理中常见的任务是识别和分析其底层状态可能发生多次变化的复杂系统。这种情况在工业系统、物理现象或人类活动被连续传感器监测时出现。从实践者的角度来看,目标是从记录的信号中提取有关被监测对象的不同状态和转换的后续有意义信息,以进行分析。这种设置涵盖了广泛的实际场景和各种信号类型。
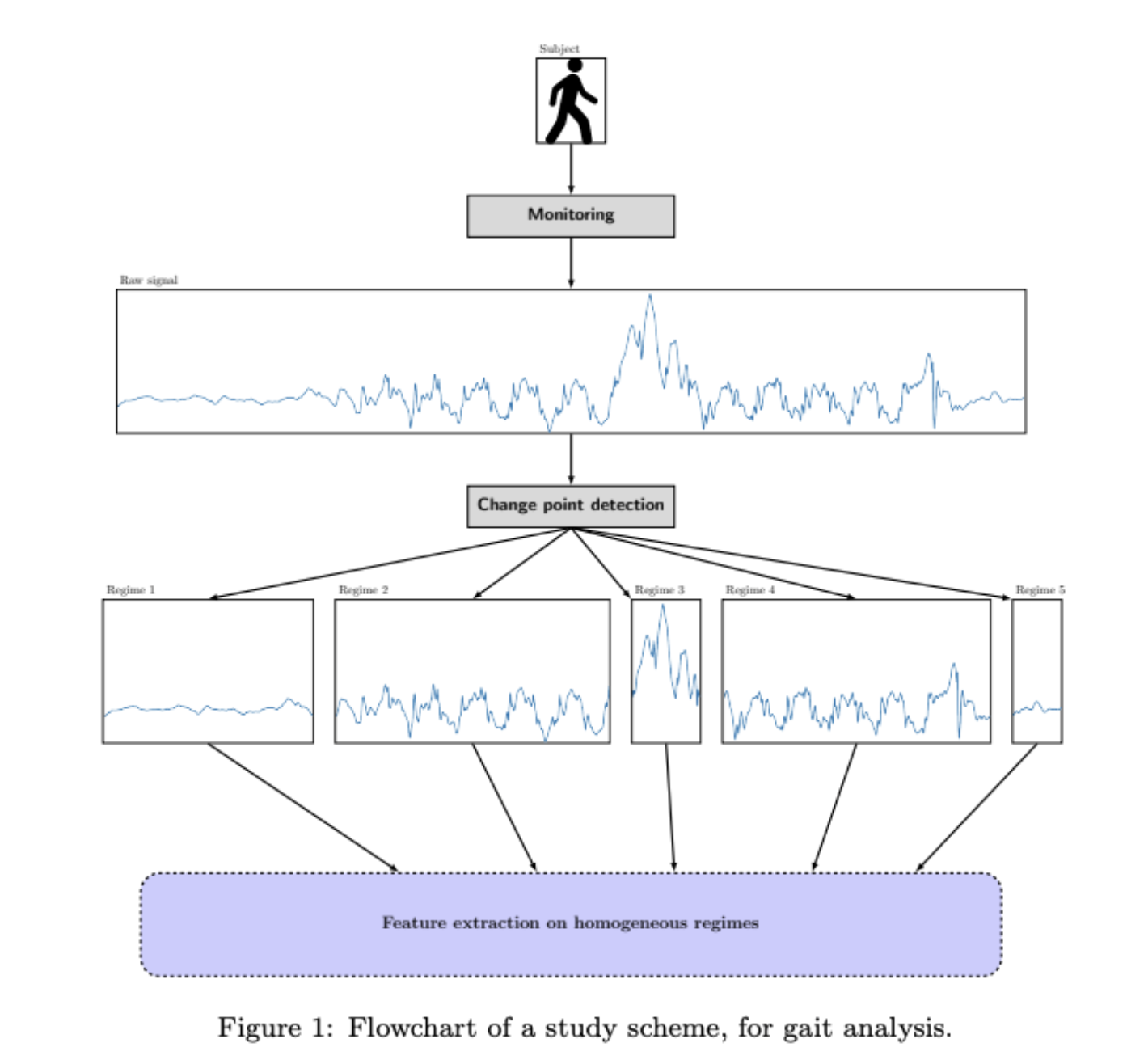
1.问题定义
拐点检测(Change Point Detection)是指在非平稳的时间序列曲线中,通过识别一些时间点(t1, t2, …, tk),这些点对应的位置发生曲线的突变。这些时间点被称为拐(Change Points),而在连续的两个拐点之间,曲线是相对平稳的。拐点检测在分析时间序列数据、理解观测现象的转变和动态变化方面非常有用。
2.符号定义
- y_a..b 表示时间点 a 和 b 之间的时间序列,因此完整信号为 y_0..T。
- 对于给定的拐点索引 t,它的关联分数为拐点分数 τ: t / T ∈ (0, 1]。
- 拐点分数的集合写作 τ = {τ_1, τ_2, …},表示所有拐点的分数。
三,研究方法
- 构造对照函数 V(t, y),目标是最小化对照函数的值。
- 对照函数 V(t, y) = ∑(k=0)^K c(y(t_k..t_(k+1))),其中 c(⋅) 是用来测量拟合度的损失函数,其值在均匀的子序列上较低,在不均匀的子序列上较高。
- 根据离散优化问题,拐点的总数量记为 K。
如果 K 是固定值,估算的拐点值为 min t =K V(t)。 - 如果 K 不是固定值,估算的拐点值为 min t V(t) + pen(t),其中 pen(t) 是对 t 的惩罚项。
- 拐点检测的算法包含三个元素:选择合适的损失函数来测算子序列的均匀程度,解决离散优化问题,合理约束拐点的数量。
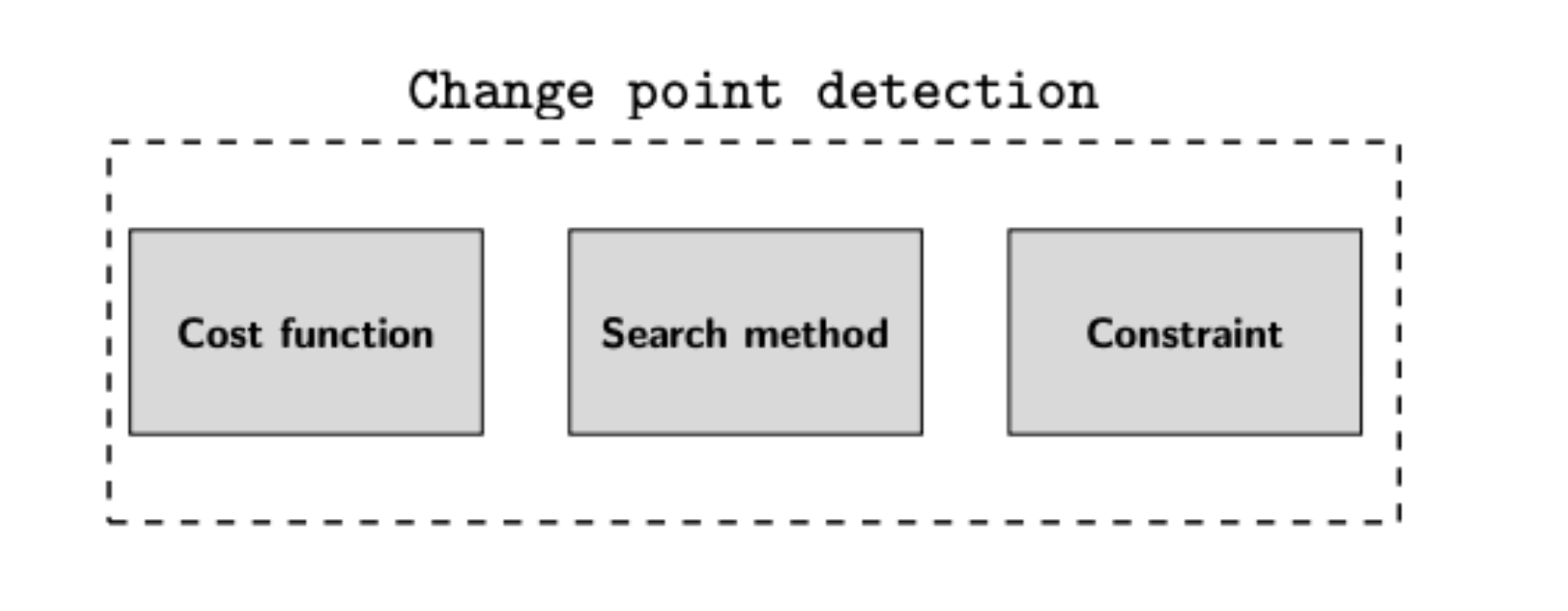
1.损失函数
1.1 损失函数定义
- 损失函数根据被检测拐点的变化类型而定。
- 对于 Piecewise i.i.d. signals,使用 i.i.d. 变量对信号进行建模。
假设 y_1, …, y_T 是独立随机变量,概率分布 f(y_t θ) 依赖于向量值参数 θ。 假设存在一系列真实的拐点 t⋆ = {t_1⋆, …},并满足 y_t ∼ ∑_(i=0)^K f(⋅ θ_k),其中 t_k⋆ < t ≤ t_(k+1)⋆。 在这种场景下,拐点检测通过最大似然估计实施,损失函数为 c_i.i.d.(y_a..b) = -sup_θ ∑_(t=a+1)^b log f(y_t θ)。
分布的选择取决于对数据的先验知识,常用的是高斯分布和一般指数族的分布。
例一:正态数据的均值漂移 均值漂移模型是拐点检测领域最常研究的模型之一。假设 y 1 , … , y T 为一系列独立的正态随机变量,具有分段常数均值和常数方差。在这种情况下,损失函数 c i . i . d . ( ⋅ ) 定义为: c L 2 ( y a . . b ) : = ∑ t = a + 1 b ∥ y t − y ‾ a . . b ∥ 2 2 其中 y ‾ a . . b 表示子信号 y a . . b 的经验均值,也称为平方误差损失。这种模型通常应用于DNA序列和地理信号处理。
例二:正态数据的均值漂移和方差漂移 这是对均值漂移模型的自然扩展,允许方差也发生突变。假设 y 1 , … , y T 为一系列独立的正态随机变量,具有分段常数均值和常数方差。在这种情况下,损失函数 c i . i . d . ( ⋅ ) 定义为: c Σ ( y a . . b ) : = log det Σ ^ a . . b 其中 Σ ^ a . . b 表示子信号 y a . . b 的经验协方差矩阵。这种损失函数可用于检测随机变量(不一定是高斯分布)在前两个时刻之间的变化,即使它服从加入 c i . i . d . ( ⋅ ) 的高斯似然。这种模型通常应用于股票市场时间序列和医药信息处理。
例三:计数数据 假设 y 1 , … , y T 为一系列独立的泊松分布随机变量,具有分段常数速率参数。这种模型的损失函数 c poisson ( ⋅ ) 定义为: c Poisson ( y a . . b ) : = − ( b − a ) y ‾ a . . b log y ‾ a . . b 这种模型常用于建模统计数据。
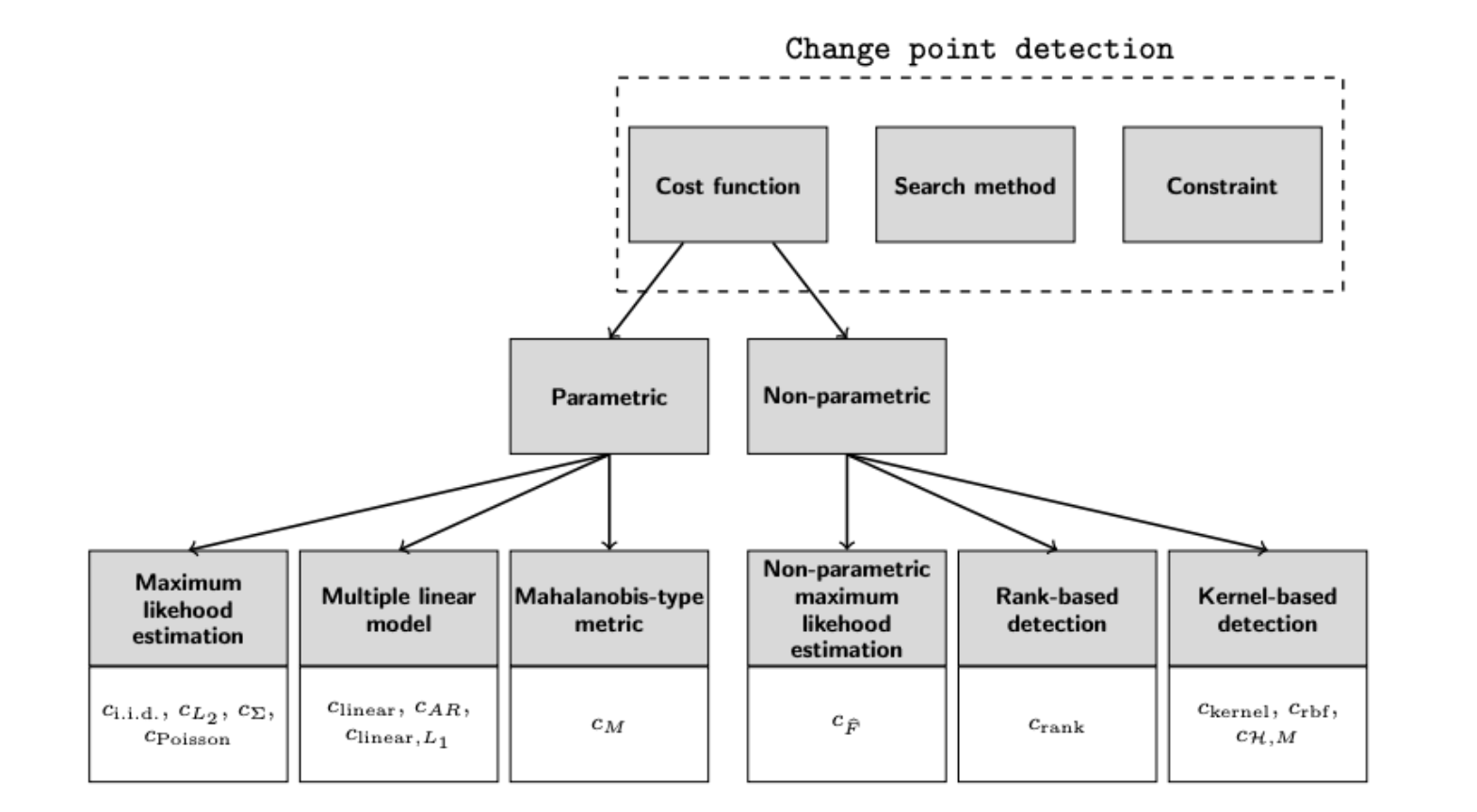
1.2 损失函数总结

2.查找算法
在拐点检测中,当拐点数量K是固定值时,可以使用离散优化算法来寻找最优的拐点集合。下面是一种基本的方法,其中对照函数V(.)用于度量拐点集合的好坏,并最小化该函数来找到最优的拐点集合。
初始化:设置初始拐点集合t为一个空集。
离散优化过程: a. 从可能的拐点位置中选择一个未被选择的位置i,将其添加到拐点集合t中。 b. 如果t的大小小于K,则返回步骤2a。 c. 如果t的大小等于K,则计算对照函数V(t, y)的值。这个函数用于评估拐点集合t的好坏程度。 d. 从t中移除一个拐点位置j,并尝试用其他未被选择的位置替换它,得到一个新的拐点集合t’。 e. 计算新的拐点集合t’的对照函数值V(t’, y)。 f. 如果V(t’, y) < V(t, y),则更新t为t’,并返回步骤2b。否则,保持t不变,返回步骤2b。
输出:最终的拐点集合t^K(y)即为最小化对照函数V(.)的结果。
在这个过程中,对照函数V(.)的选择对于拐点检测的性能至关重要。常见的对照函数包括平方误差损失、绝对误差损失、似然函数等,具体的选择取决于信号的特点和应用场景。
需要注意的是,这只是一个基本的离散优化方法,可能存在局部最优解的问题。为了得到更好的结果,可以考虑使用不同的优化算法,如遗传算法、模拟退火算法等,并进行参数调优以提高性能。
以上提到的方法是一种常见的离散优化算法,用于固定拐点数量K的拐点检测。具体实施时,根据具体的问题和数据特点,可能需要进行适当的修改和调整。
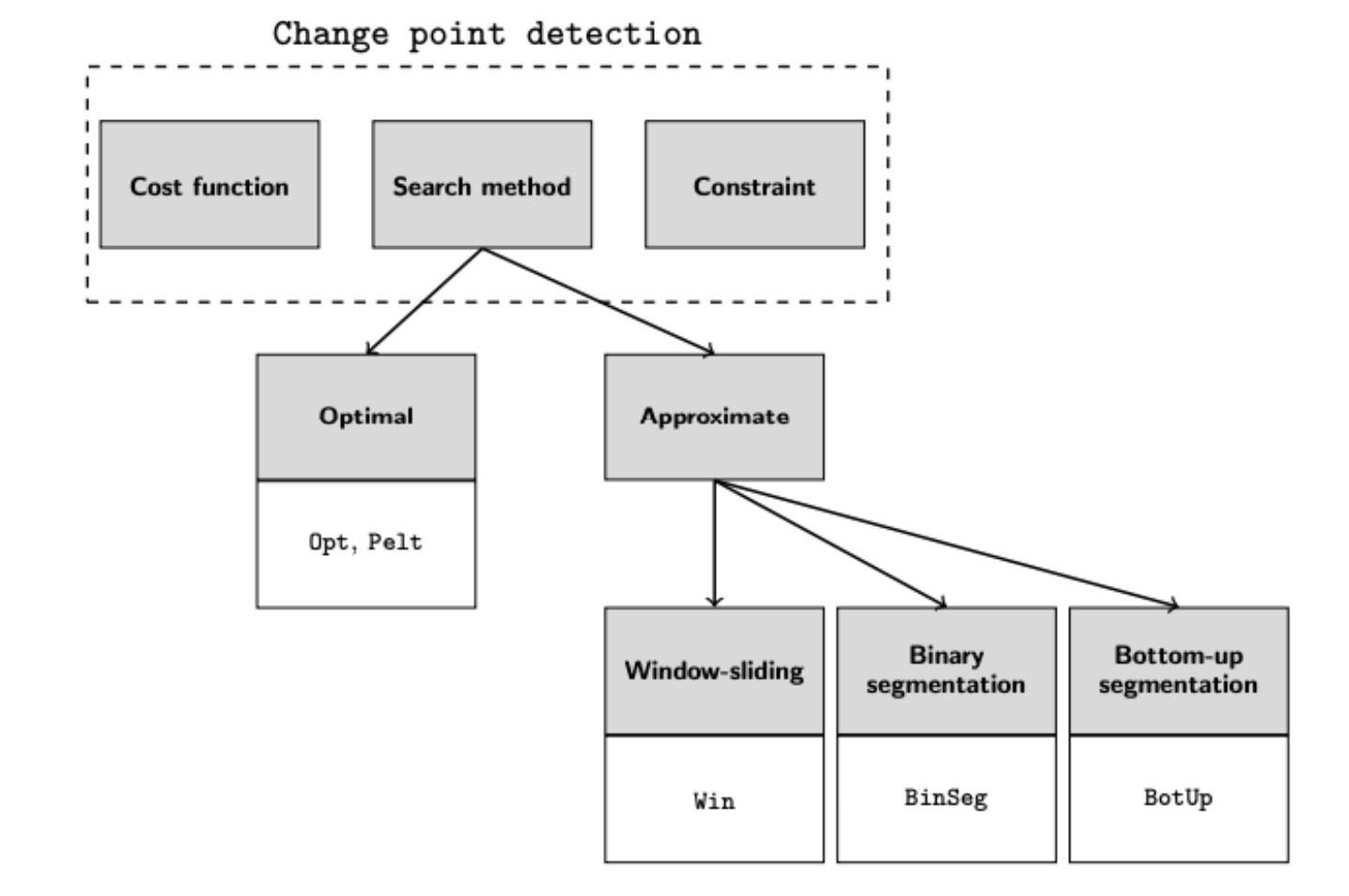
2.1 最优检测
应用于固定K的拐点查找算法是在索引集合{1, …, T}上的离散优化问题。所有可能的组合基数为(T-1 choose K),数量太多使得无法进行全面的遍历。但可以使用动态规划的方法来有效解决,本文将该算法记作Opt。
实际上,动态规划依赖于目标函数V(.)的附加性质。粗略地说,它包括递归地解决子问题,并满足以下观察结果:
min|t|=K V(t, y=y0..T) = min0=t0<t1<⋯<tK<tK+1=T ∑k=0K c(ytk..tk+1) = min t≤T-K [c(y0..t) + min t=t0<t1<⋯<tK-1<tK=T ∑k=0K-1 c(ytk..tk+1)] = min t≤T-K [c(y0..t) + min|t|=K-1 V(t, yt..T)].
直观地看,公式表明如果已知由K-1个元素组成的最优子信号{ys}tT,计算第一个拐点是容易的。接下来,可以通过递归地执行上述观察结果来得到完整的集合。结合二次误差损失函数的计算,Opt算法的复杂度为O(KT^2)。使用更复杂的损失函数会增加计算的复杂度。由于Opt算法的复杂度是二次的,因此适用于较短的信号,一般包含大约一百个样本点。
对于对降低Opt算法计算负担的方法感兴趣的读者,可以参考Rigaill和Yann在论文中提供的几种方法。

2.2 滑动窗口
滑动窗口算法(以下简称Win)是一种快速近似的Opt替代算法,它依赖于单个变化点检测程序,并通过扩展该程序来找到多个变化点。算法的实现中,两个相邻的窗口沿着信号滑动,计算第一个窗口和第二个窗口之间的差异。对于给定的损失函数,两个子信号之间的差异可以表示为:d(ya..t, yt..b) = c(ya..b) - c(ya..t) - c(yt..b) (1 ≤ a < t < b ≤ T).
当这两个窗口包含不相似的片段时,计算得到的差异值将会很大,从而可以检测到一个拐点。在离线设置中,可以计算完整的差异曲线,并执行峰值搜索过程以找到拐点的索引。
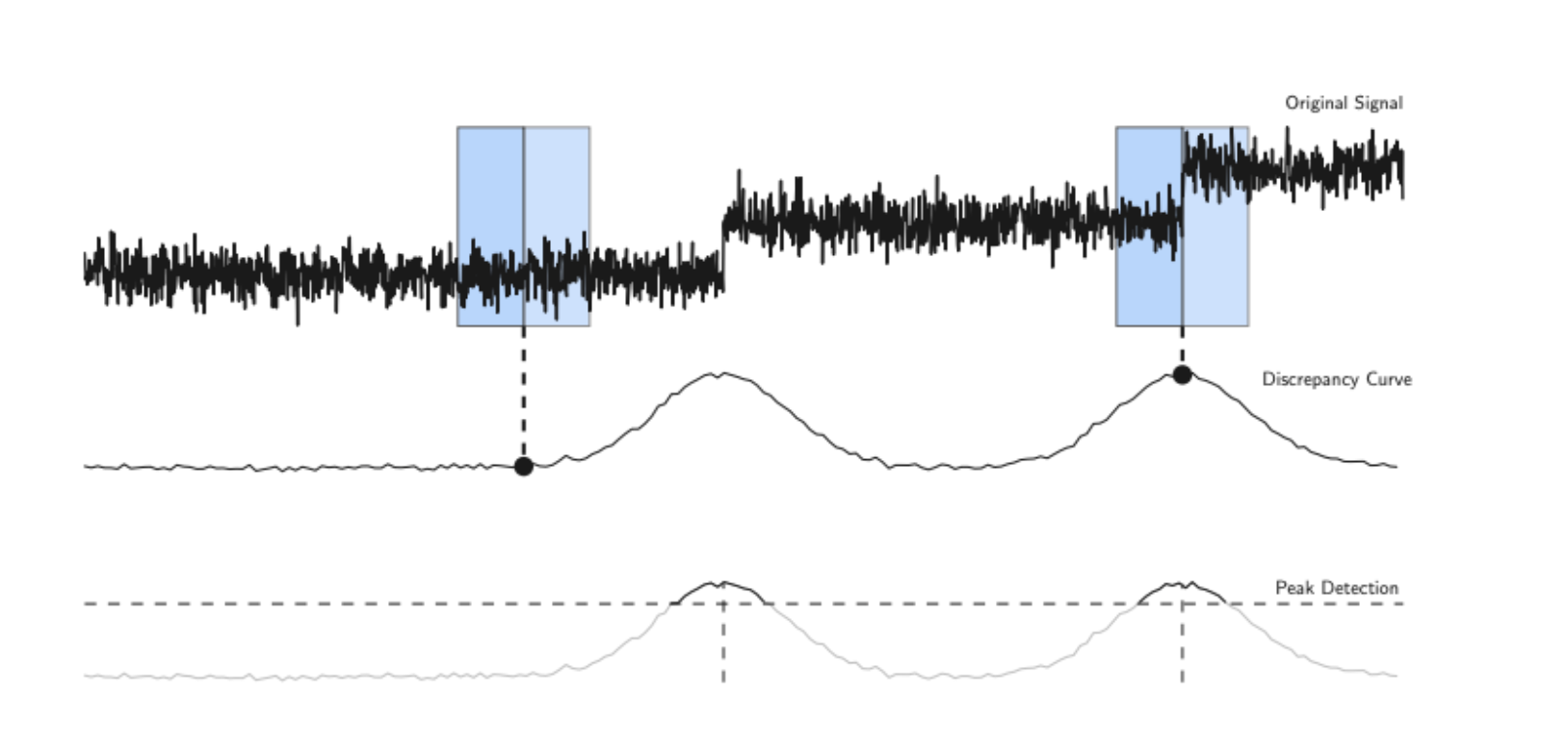
类似的,还有一种方法叫做双样本检验(或同质性检验)two-sample test (or homogeneity test),它是一种统计假设检验程序,用于评估两个样本群体的分布是否相同。
滑动窗口算法(Win)的最大优点是复杂性低(与损失函数 cL2配合时为线性时间),易于实现。此外,任何单一拐点检测方法都可以加入到该方案中。有大量参考文献提供了用于不同成本函数的差异的渐近分布,这对于在峰值搜索过程中找到适当的阈值非常有用。然而,滑动窗口算法通常不稳定,因为单个变化点检测是在小区域(窗口)上进行的,这降低了它的统计功效。
伪代码

2.3 二分分割
二分分割(BinSeg)也是一种快速近似的Opt的替代算法,在拐点检测的用场景中,BinSeg是最常用的方法之一,因为它的概念简单且易于实现。
BinSeg是一种顺序贪心算法,每次迭代中执行单个变化点的检测并生成估计值t^(k)。在下文中,上标k表示顺序算法的第k步。算法的示意图如下:
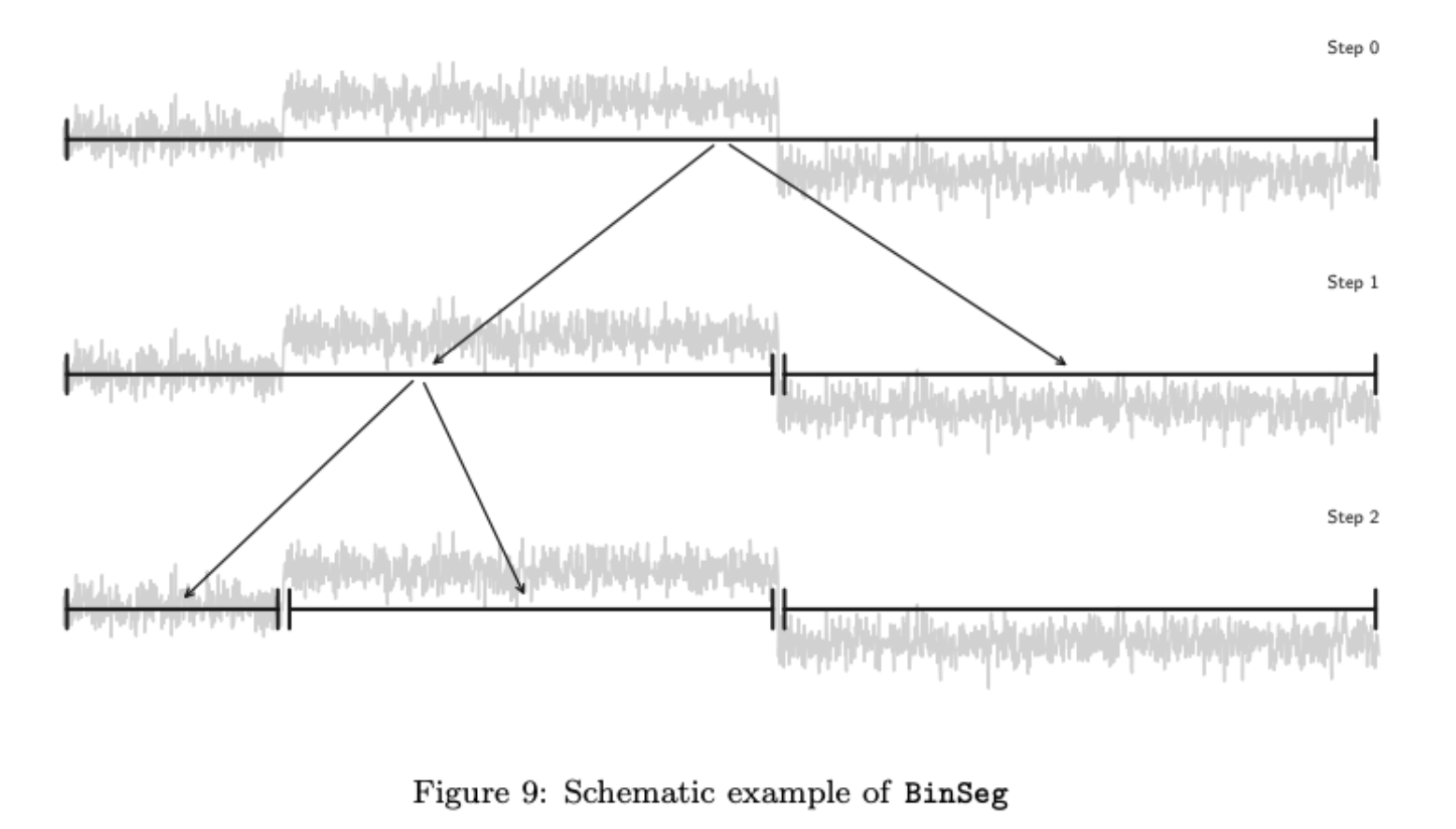
第一个估计的拐点\hat{t}^{(1)}t^(1)为:
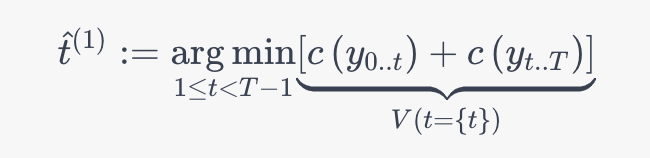
这个操作是贪心的,目的是找出使得总体损失最小的拐点。然后,在\hat{t}^{(1)}t^(1)的位置将信号分成了两部分,并对得到的子信号进行相同的操作,直到找不到更多的拐点为止。
在BinSeg的第k次迭代之后,下一个估算的拐点\hat{t}^{(k+1)}t^(k+1)属于原始信号的k+1个子片段之一,计算公式为
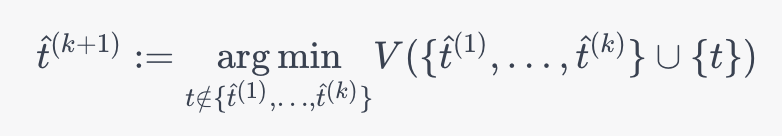
由于K的总数是已知的,因此BinSeg需要执行K步来估算所有的拐点。贪心检测的过程可以设计为一个双样本检验的过程。
在使用二次损失误差C_{L_{2}}CL2的情况下,BinSeg的复杂度为O(T \log T)O(TlogT)。
从理论上讲,BinSeg被证明可以在均值模型下用二次误差C_{L_{2}}CL2产生渐近一致的估计。更近期的结果表明,只有当任何两个相邻变化点之间的最小间距大于T^{3/4}T3/4时,BinSeg才能一致地检测到拐点。一般来说,BinSeg的输出只是最优解的近似值,尤其是不能精确地检测到接近的拐点,原因在于估计的拐点\hat{t}^{(k)}t^(k)不是从均匀分段估计的,并且每个估计都取决于先前的分析。
伪代码:

2.4 自底向上分割
自底向上分割是 BinSeg 的自然对应,下文记作 BotUp,这种算法同样也是一种近似算法。跟 BinSeg 相反,BotUp 最开始就把源信号分割成很多子信号,然后序列化的把它们合并直到剩下 K 个拐点。 在每个步骤中,所有潜在的变化点(分隔相邻子段的索引)按它们分开的段之间的差异进行排序。差异性最小的拐点被删除,由它分割的两个子段被合并。跟 BinSeg 的贪心算法相反,BotUp 被称为一种“慷慨”的算法。
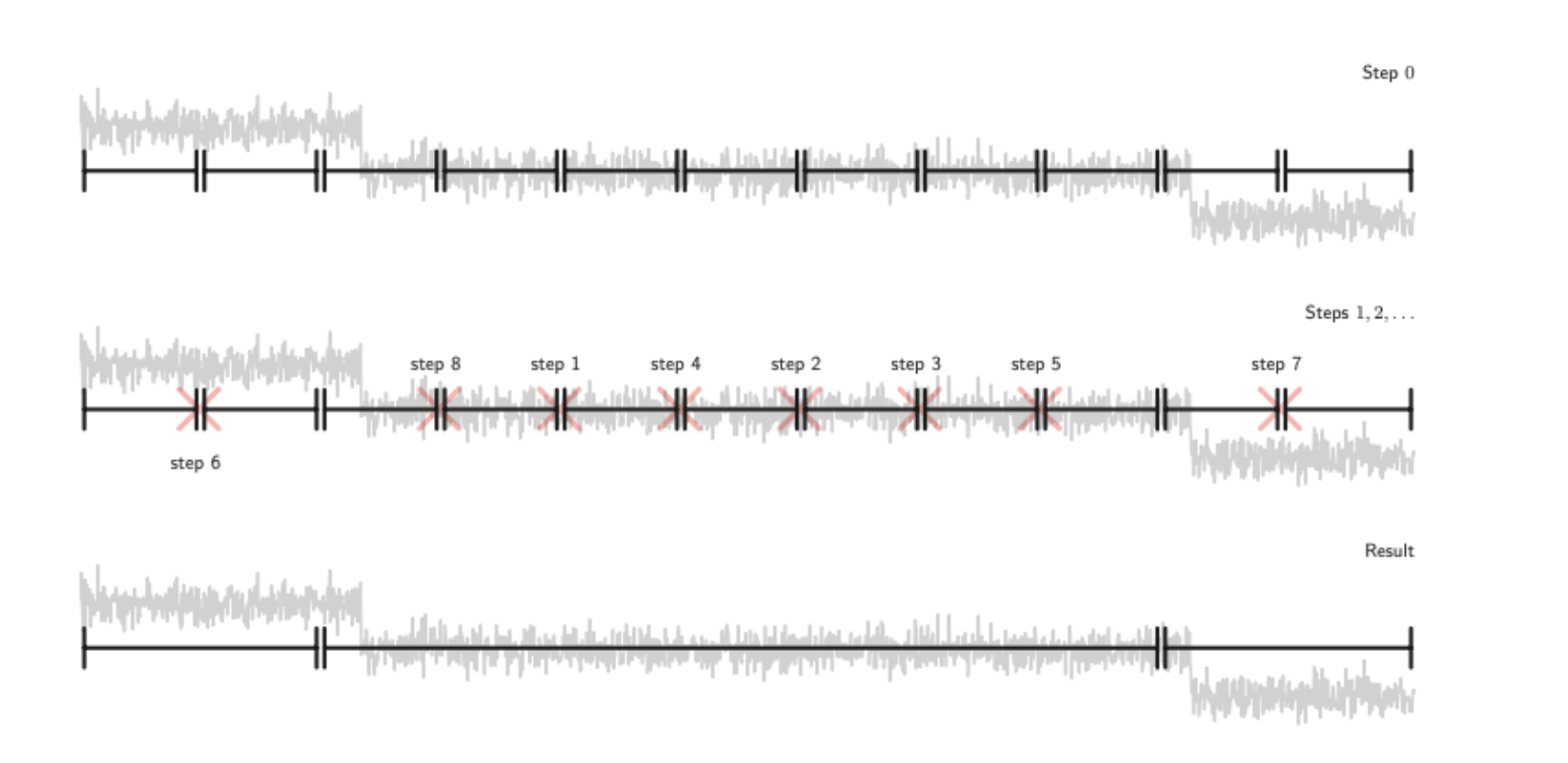
对于给定的损失函数,两个子信号的差异性为:
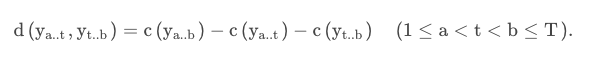
BotUp 的优势在于线性复杂度以及概念的简单性。但是它也存在一些问题:
1.如果实际的拐点不在最开始划分出来的点集中,那么 BotUp 也永远不会考虑它。
2.在第一次迭代中,融合过程可能是不可靠的,因为计算只是在小的区段上进行,统计意义比较小。
3.在现有文献中,BotUp 的研究不如 BinSeg,没有理论收敛性研究 theoretical convergence study 可用。

3.限制项
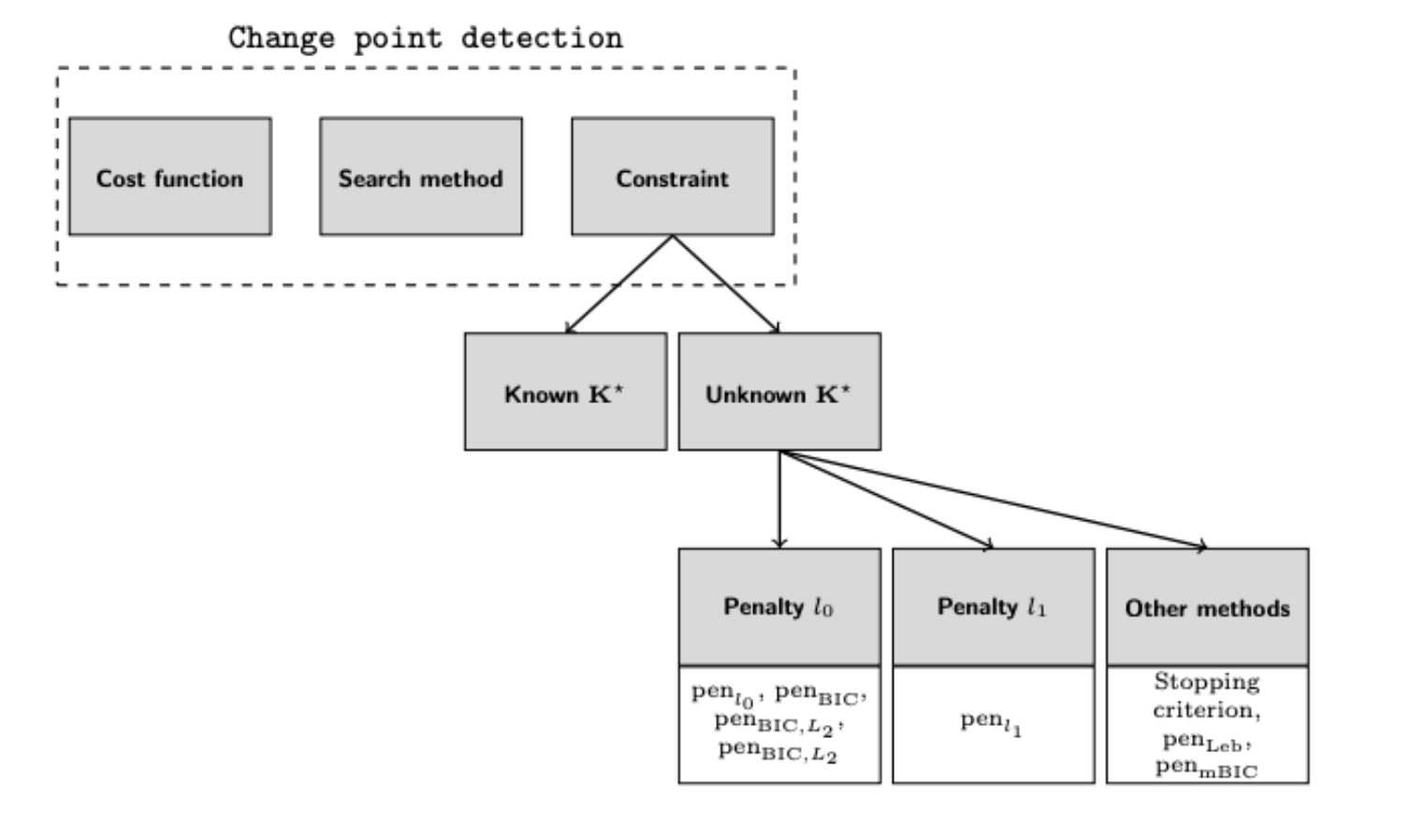
3.1 l0 惩罚项
| 惩罚项也被称为线性惩罚项,被认为是最流行的惩罚项。一般而言,l0惩罚项记作penl0,公式为:penl0(t) := β | t | ,其中β > 0,负责权衡复杂性和拟合度。当出现的拐点越来越多时,它平衡了总成本V(⋅)减少的幅度。有很多利用这个规则的例子,最著名的是BIC(Bayesian Information Criterion)和AIC(Akaike Information Criterion)。 |
| 假设对信号y有一个分段i.i.d.模型,设定c = ci.i.d,对于给定的一组拐点t,引出BIC的约束似然公式为:2V(t) + plogT | t | ,其中p为参数空间parameter space的维度(如p = 1表示平均值的单变量变化,p = 2表示平均值和极差的单变量变化等等)。因此,BIC等同于当β = p / 2 logT时的线性惩罚拐点检测:penBIC(t) := (p / 2) logT | t | 。 |
| 类似的,在固定方差的均值飘逸模型下(mean-shift model with fixed variance),c = cL2,BIC惩罚项为:penBIC, L2(t) := σ^2 logT | t | 。 |
| AIC也是类似的,公式为:penAIC, L2(t) := σ^2 | t | 。 |
从理论上讲,拐点估计的一致性在某些情况下是可以证明的。研究最多的模型是均值漂移模型,当满足下列假设时,其估计的拐点数和拐点分数概率渐近收敛。
3.2 Pelt 算法
实施线性惩罚项拐点检测的一个朴素的实施方案是对足够大的 Kmax, 对K = 1…..Kmax都进行执行 Opt,然后找出使得惩罚结果最小的部分,但是这种方案的平方复杂度是难以接受的,因此我们需要实施其他复杂度更低的方法。
Pelt 算法 Pruned Exact Linear Time 可以用于找出准确解,该方法按顺序考虑每个样本,并基于明确的修剪规则决定是否从潜在的拐点集中丢弃它。假设片段长度是从均匀分布中随机选取的,Pelt 的复杂度是 O ( T ) \mathcal{O}(T)O(T),尽管这种设定是不现实的(会产生短片段),但 Pelt 依然比上述的朴素启发式快几个数量级。
使用 Pelt 时唯一需要调整的参数只有惩罚级别 β \betaβ,β \betaβ 的设定至少与样本数和信号维度有关,β \betaβ 值越小,算法对变化的感知越敏感,可以选用较小的值来找到更多的拐点,也可以使用较大的值来仅关注显著变化。
3.3 l1 惩罚项
为了进一步降低具有线性惩罚的变化点检测的计算成本,已经提出了一种将l0惩罚项转换为l1惩罚项的替代公式。类似的替代公式在机器学习的许多发展中起到了至关重要的作用,如稀疏回归、压缩感知和稀疏PCA。在数值分析和图像去噪中,这种惩罚项也被称为总变差正则项。
引入这种策略的目的是检测带有高斯噪声的分段常量信号中的均值漂移现象。相关的损失函数是CL2,对于这种设定,拐点检测优化问题可以表示为:
| min t V(t) + β∑k=1 | t | ȳtk-1..tk - ȳtk..tk+1 | 1, |
其中ȳtk-1..tk是子信号ytk-1..tk的经验均值。因此,l1惩罚项可以表示为:
| penl1(t) := β∑k=1 | t | ȳtk-1..tk - ȳtk..tk+1 | 1。 |
实际上,有文献指出,这等同于一个凸优化问题。对于矩阵Y := [y1, …, yT]′ ∈ RT×d,S ∈ RT×T-1,并且定义矩阵S的元素为:
Sij := { 1 if i > j, 0 if i ≤ j }。
Ȳ和Ṡ表示对矩阵Y和S进行每列中心化后得到的矩阵,每列中心化表示矩阵的每一列的每个元素减去该列的均值。
四,ruptures 工具库
1. ruptures特征
一个比较优秀的库是由 Charles Truong 等人开源的 ruptures 。本文简单介绍了 ruptures 的基本特性,更多详细介绍以及使用手册请阅读官方文档。
ruptures 的流程结构如图所示:
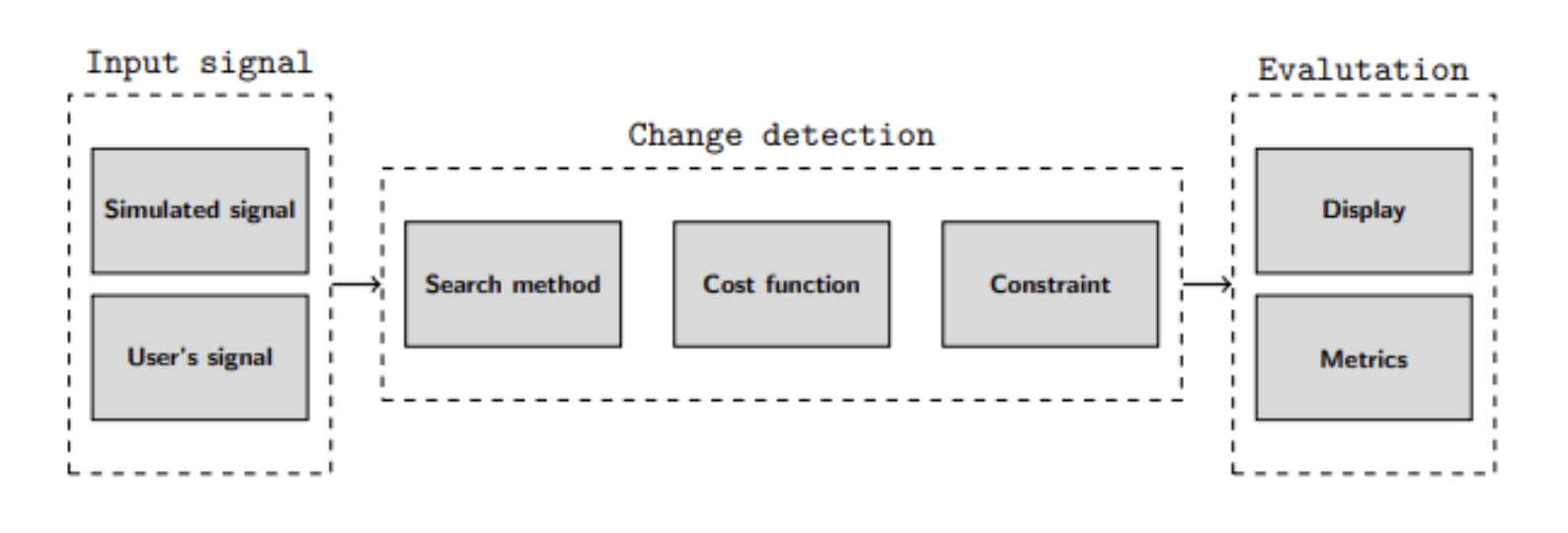
2. ruptures特性
Search methods
ruptures 库包含了上文提到的主要查找算法,比如动态规划 dynamic programming,基于 l0 约束的检测 detection with a l0 constraint,二元分割 binary segmentation,自下而上的分割 bottom-up segmentation 以及基于窗口的分割 window-based segmentation
Cost function
在 ruptures 库中,可以选用有参损失函数 parametric cost functions 来检测标准统计量 standard statistical quantities 的变化,如均值 mean,规模 scale,维度间的线性关系 linear relationship between dimensions,自回归系数 autoregressive coefficients 等。也可以使用无参损失函数 non-parametric cost functions (Kernel-based or Mahalanobis-type metric) 来检测分布式变化。
Constraints
无论拐点数量是否已知,上述方法都适用,需要注意的是,ruptures 在成本运算 cost budget 和线性惩罚项 linear penalty term 的基础上实现拐点检测。
Evaluation
评估指标可用于定量比较分割,以及用可视化的方法评估算法性能
Input
ruptures 能在可以转化为 Numpy array 的任何信号上实施,包括单因素信号和多因素信号 univariate or multivariate signal 和Consistent interface and modularity
离散优化方法和损失函数是拐点检测的两个主要组成部分,这些在 ruptures 中都是具体的对象,因此本库的模块化程度很高,一旦有新的算法产生,即可无缝的集成到 ruptures 中。
Scalability
数据探索通常需要使用不同的参数集多次运行相同方法。 为此,实现高速缓存以将中间结果保留在内存中,从而大大降低了在相同信号上多次运行相同算法的计算成本。
ruptures 还为具有速度限制的用户提供了信号采样和设置拐点最小距离的可能
